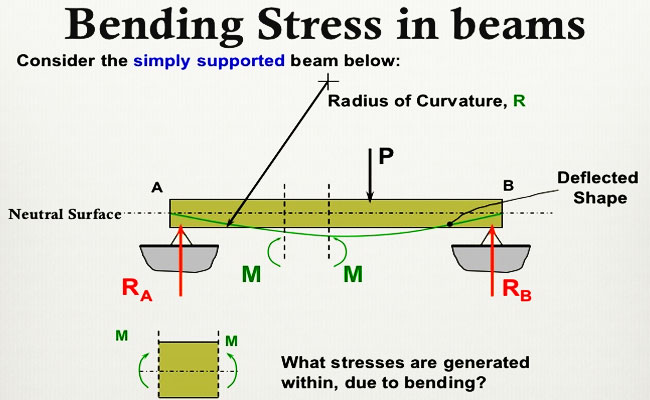
How to calculate bending stresses in beam

Compressive and tensile forces happen towards the beam axis beneath bending loads. These forces produce stresses on the beam. The extreme compressive stress is originated at the topmost edge of the beam whereas the utmost tensile stress is found at the lower edge of the beam. Bending stresses belong to indirect normal stresses.
Formula for calculating Bending Stresses in Beams or Derivation of Elastic Flexural:
If it is required to estimate the value of bending stresses evolved in a loaded beam, assume the two cross-sections of a beam as HE and GF, initially parallel as demonstrated in fig 1(a) in the video. While bending the beam, it is anticipated that these sections stay parallel i.e. H'E' and G’F’, the final location of the sections, still remain as straight lines and then they subtend some angle q.
Now, suppose fiber AB in the material, at a span y from the N.A, if the beam bends, it will extend to A'B'
As CD and C'D' remain on the neutral axis and it is anticipated that the stress on the neutral axis is zero. Consequently, no strain exists on the neutral axis.
Suppose any arbitrary a cross-section of beam, as demonstrated above now the strain on a fibre at a distance ‘y' from the N.A, is specified with the expression.
Now the term stands for the property of the material and is defined as a second moment of area of the cross-section and is demonstrated with a symbol I.
This equation is called as the Bending Theory Equation. The above proof includes the theory of pure bending without any existence of shear force. So, it is described as the pure bending equation. This equation provides distribution of stresses which are typical to cross-section i.e. in x-direction.