Alex Tomanovich has developed BEAMANAL 2.5. It is MS-Excel based powerful spreadsheet program that can be used for structural analysis. It can make analysis of either single-span or continuous-span beams depending on virtually different types of loading configurations. It involves four (4) types of single-span beams and two (2) through (5) span, continuous-span beams.The calculation is particularly made for beam end reactions along with the maximum moments and deflections.

The software cretes the plots of all of the diagrams together with a tabulation of the shear, moment, slope, and deflection for the beam or every individual span. To deal with structural steel single-span beams, an AISC 9th Edition (ASD) Code check is carried out for X-axis bending and shear.

Program Assumptions and Constraints:-

1. This program is developed on the basis of the following:

"Modern Formulas for Statics and Dynamics, A Stress-and-Strain Approach" by Walter D. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978), pages 11 to 21.

2. For the basis of analysis, the program employs the following three assumptions

• Beams should be associated with constant cross section (E and I are constant for complete span length).
• Deflections should not considerably modify the geometry of the problem.
• Stress should prevail inside the "elastic" region.

3. On the beam or every individual span, this program can manage a comple length uniform load and equal to eight (8) partial uniform, triangular, or trapezoidal loads, equal to fifteen (15) point loads, and equal to four (4) applied moments.

4. For single-span beams, this program constantly assumes a specific orientation for two (2) of the the four (4) different types. Particularly, the fixed end of both a "propped" or "cantilever" beam is always considered to exist on the right end of the beam.

5. This program can work out the beam end vertical reactions and moment reactions (if relevant), the maximum positive moment and negative moment (if relevant), and the maximum negative deflection and positive deflection (if relevant). The values are computed for the end reactions and maximum moments and deflections and these are obtained by segregating the beam into fifty (50) equivalent sections with fifty-one (51) points along with all of the point load and applied moment locations also. (Note: the actual point of maximum moment happens if the shear = 0, or goes through zero, whereas the actual point of maximum deflection is where the slope = 0.)

Download Structural Analysis Spreadsheet

Article Source
www.cesdb.com

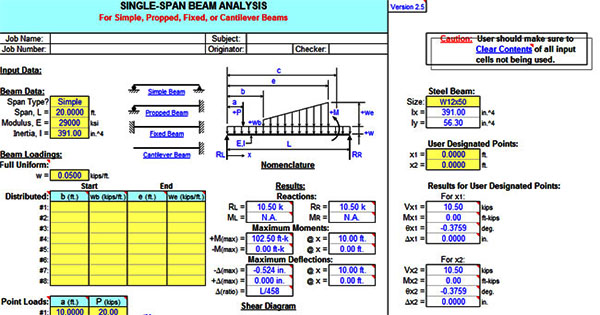
Image Courtesy : www.cesdb.com