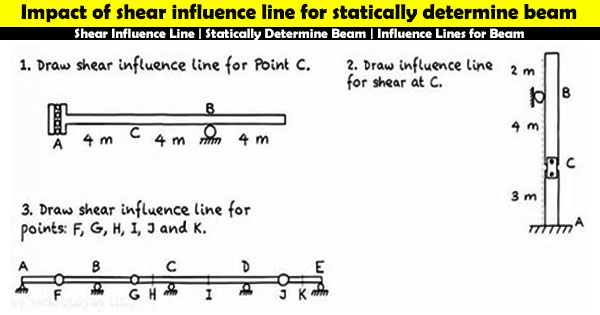
Impact of shear influence line for statically determine beam

This construction video briefly explains shear influence line for statically determinate beam. While designing hinge for any bridge that bears moving load, it is required to find out the highest shear force to be resisted by hinge. The force can be readily determined by drawing an influence line.
The basic meaning for the determinate beam is that the beam in which unidentified support reactions are computed through static equilibrium equations only.
Actually structures are termed as determinate or indeterminate on the basis of their loading and support reaction conditions.
A beam remains as a structural member and its determinacy and indeterminacy is completely influenced by the type of supports provided.
A statically determinate structure belongs to one in which reactions and internal forces are set completely with free-body diagrams and equations of equilibrium. These equations range from Σ H = 0, Σ V = 0 and Σ M = 0. It must be remembered that the results of analysis are not reliant on the material which develop the structure.
In order to analyze a statically determinate beam, the first step is to determine the reactions. Based on the reactions, the internal forces can be set up with equilibrium-based procedures. These forces produce deformations that result in dislocating the beam.
In engineering, an influence line for any specified point or section of structure (beam, truss etc.) stands for a diagram whose ordinates denote to measure the variation of a function like shear force, bending moment, deflection etc at a point or section, while the unit load is located at any point along the structure.
Some of the common functions calculated with influence lines are reactions, shear, moment, and deflection. Influence lines are essential for designing beams and trusses applied in bridges, crane rails, conveyor belts, floor girders, and other structures where loads will interchange along their area. The influence lines display where a load will produce the maximum influence for any of the functions studied.
For more information, watch the following video and view its contents.